Odnośniki, wykresy, statystyki i tabele przestawne

Po zapoznaniu się z podstawowymi funkcjami, odwołaniami do komórek oraz funkcjami daty i czasu, teraz zagłębimy się w niektóre z bardziej zaawansowanych funkcji programu Microsoft Excel. Prezentujemy metody rozwiązywania klasycznych problemów w finansach, raportach sprzedaży, kosztach wysyłki i statystykach.

NAWIGACJA SZKOLNA

1. Dlaczego potrzebujesz formuł i funkcji??
2. Definiowanie i tworzenie formuły
3. Względne i bezwzględne odwołanie do komórki i formatowanie
4. Przydatne funkcje, które powinieneś poznać
5. Odnośniki, wykresy, statystyki i tabele przestawne

Te funkcje są ważne dla biznesu, studentów i osób, które chcą po prostu więcej się nauczyć.

VLOOKUP i HLOOKUP

Oto przykład ilustrujący funkcje wyszukiwania pionowego (VLOOKUP) i poziomego (HLOOKUP). Funkcje te są używane do przetłumaczenia liczby lub innej wartości na coś, co jest zrozumiałe. Na przykład możesz użyć VLOOKUP, aby pobrać numer części i zwrócić opis przedmiotu.

Aby zbadać tę sprawę, wróćmy do arkusza kalkulacyjnego "Decision Maker" w części 4, gdzie Jane próbuje zdecydować, co nosić do szkoły. Ona nie jest już zainteresowana tym, co nosi, ponieważ wylądowała nowego chłopaka, więc będzie teraz nosić przypadkowe stroje i buty.

W arkuszu kalkulacyjnym Jane wymienia stroje w pionowych kolumnach i butach, poziome kolumny.

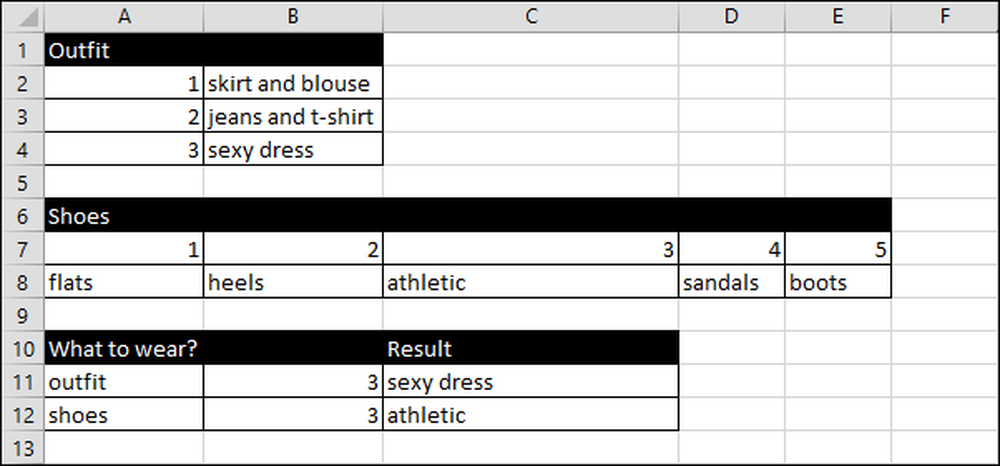
Otwiera arkusz kalkulacyjny, a funkcja RANDBETWEEN (1,3) generuje liczbę równą 1 lub 3 odpowiadającą trzem rodzajom strojów, które może nosić.

Używa funkcji RANDBETWEEN (1,5) do wyboru spośród pięciu rodzajów butów.

Ponieważ Jane nie może nosić numeru, musimy przekonwertować go na nazwę, dlatego używamy funkcji wyszukiwania.

Używamy funkcji VLOOKUP, aby przetłumaczyć numer stroju na nazwę stroju. HLOOKUP przekłada się z liczby butów na różne typy obuwia w rzędzie.

Arkusz kalkulacyjny działa w ten sposób w przypadku strojów:

Excel wybiera losową liczbę od jednego do trzech, ponieważ ma trzy opcje wyposażenia.

Następnie formuła tłumaczy liczbę na tekst za pomocą funkcji = VLOOKUP (B11, A2: B4,2), która używa liczby losowej wartości z B11 do wyszukiwania w zakresie A2: B4. Następnie daje wynik (C11) z danych wymienionych w drugiej kolumnie.

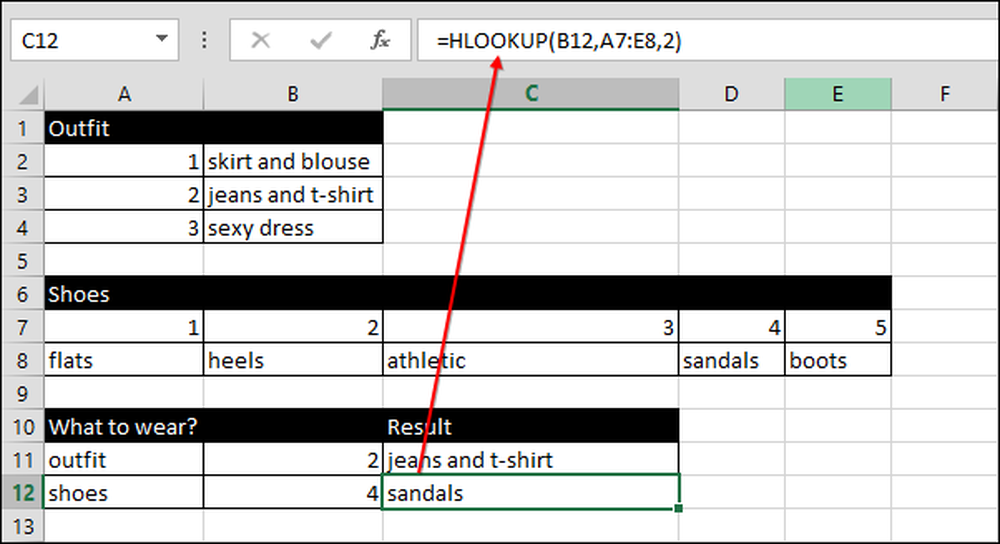
Używamy tej samej techniki do wybierania butów, z tą różnicą, że używamy VOOKUP zamiast HLOOKUP.

Przykład: podstawowe statystyki

Prawie wszyscy znają jedną formułę ze statystyk - średnia - ale są jeszcze inne statystyki istotne dla biznesu: odchylenie standardowe.

Na przykład, wiele osób, które poszły na studia, zadręczało się swoim wynikiem SAT. Mogą chcieć wiedzieć, jak mają rangę w porównaniu do innych uczniów. Również uniwersytety chcą o tym wiedzieć, ponieważ wiele uniwersytetów, szczególnie prestiżowych, odrzuca uczniów z niskimi wynikami SAT.

Jak więc my lub uniwersytet mierzymy i interpretujemy wyniki SAT? Poniżej przedstawiono wyniki SAT dla pięciu studentów w zakresie od 1 870 do 2 230 osób.

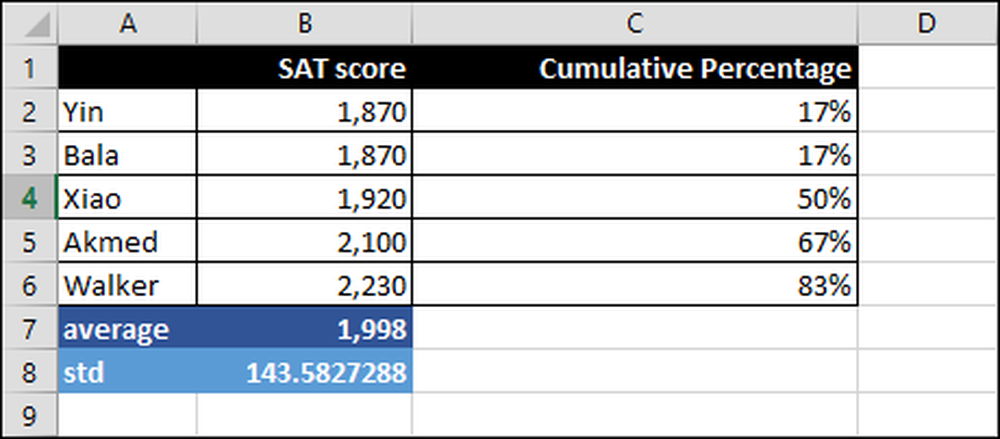
Ważne liczby do zrozumienia to:

Średni - Średnia jest również określana jako "średnia".

Odchylenie standardowe (STD lub σ) - Liczba ta pokazuje, jak szeroko rozproszony jest zbiór liczb. Jeśli odchylenie standardowe jest duże, liczby są daleko od siebie, a jeśli są zerowe, wszystkie liczby są takie same. Można powiedzieć, że odchylenie standardowe jest średnią różnicą pomiędzy wartością średnią a obserwowaną wartością, tj. 1,998 i każdym wynikiem SAT. Należy pamiętać, że powszechne jest skracanie odchylenia standardowego za pomocą greckiego symbolu sigma "σ".

Ranking procentowy - Kiedy uczeń otrzymuje wysoki wynik, może pochwalić się, że jest w 99 percentylu lub coś podobnego. "Ranking procentowy" oznacza, że ​​procent wyników jest niższy niż jeden konkretny wynik.

Odchylenie standardowe i prawdopodobieństwo są ściśle ze sobą powiązane. Można powiedzieć, że dla każdego odchylenia standardowego prawdopodobieństwo lub prawdopodobieństwo, że liczba ta mieści się w tej liczbie standardowych odchyleń, wynosi:

STD	Procent wyników	Zakres wyników SAT
1	68%	1,854-2,142
2	95%	1,711-2,285
3	99,73%	1,567-2,429
4	99,994%	1 424-2,572

Jak widać, szansa, że ​​każdy wynik SAT jest poza 3 STD jest praktycznie zero, ponieważ 99,73 procent wyników jest w ciągu 3 STD's.

Teraz spójrzmy na arkusz kalkulacyjny ponownie i wyjaśnij, jak to działa.

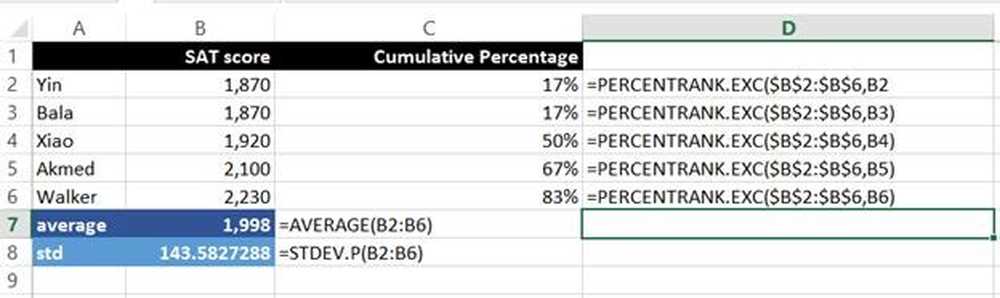
Teraz wyjaśniamy formuły:

= AVERAGE (B2: B6)

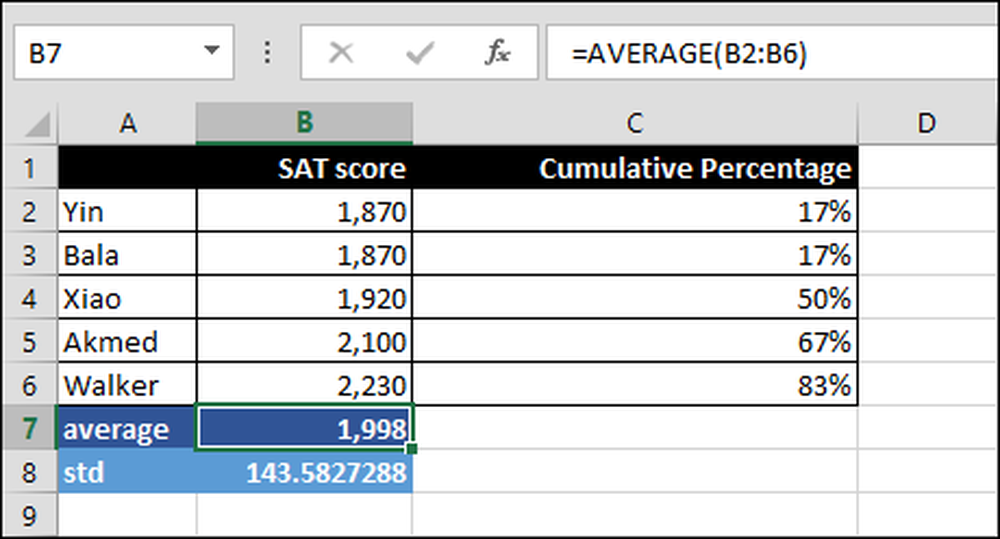
Średnia wszystkich wyników w zakresie B2: B6. W szczególności suma wszystkich wyników podzielona przez liczbę osób, które przystąpiły do ​​testu.

= STDEV.P (B2: B6)

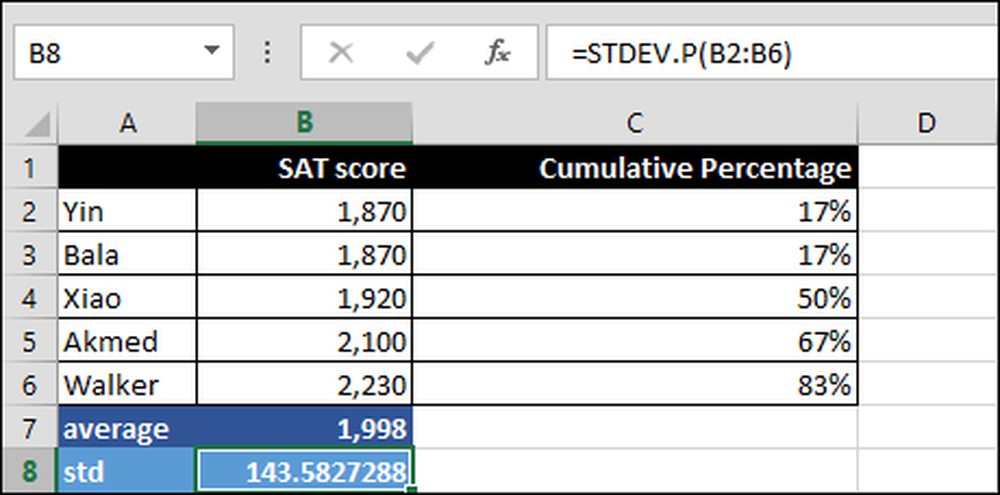
Odchylenie standardowe w zakresie B2: B6. ".P" oznacza STDEV.P jest używany do wszystkich wyników, tj. Do całej populacji, a nie tylko do podzbioru.

= PERCENTRANK.EXC ($ B 2: $ B 6 $, B2)

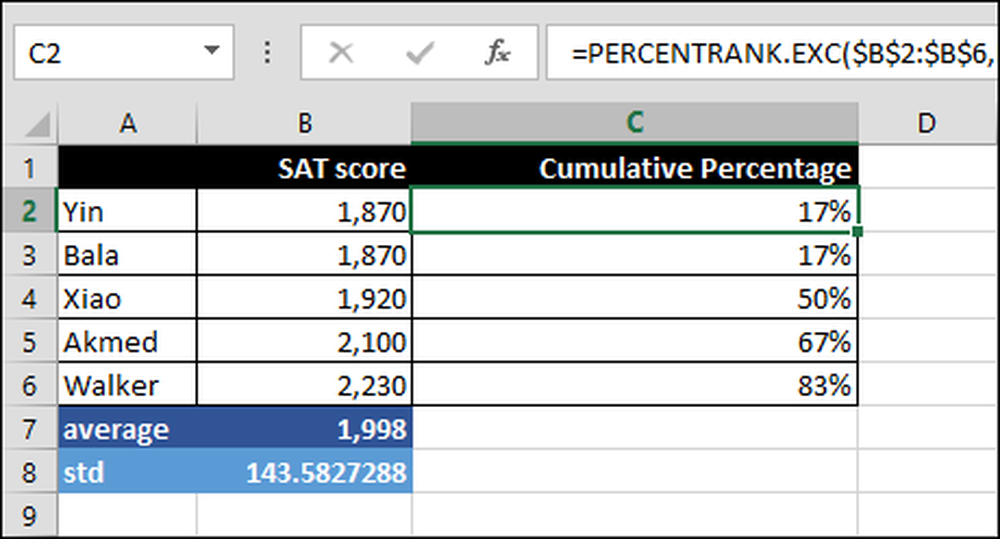
Oblicza on skumulowany odsetek w zakresie B2: B6 na podstawie wyniku SAT, w tym przypadku B2. Na przykład 83 procent wyników jest poniżej wyniku Walkera.

Wykresy wyników

Umieszczenie wyników na wykresie ułatwia zrozumienie wyników, a ponadto możesz pokazać je w prezentacji, aby lepiej wyrazić swoje zdanie.

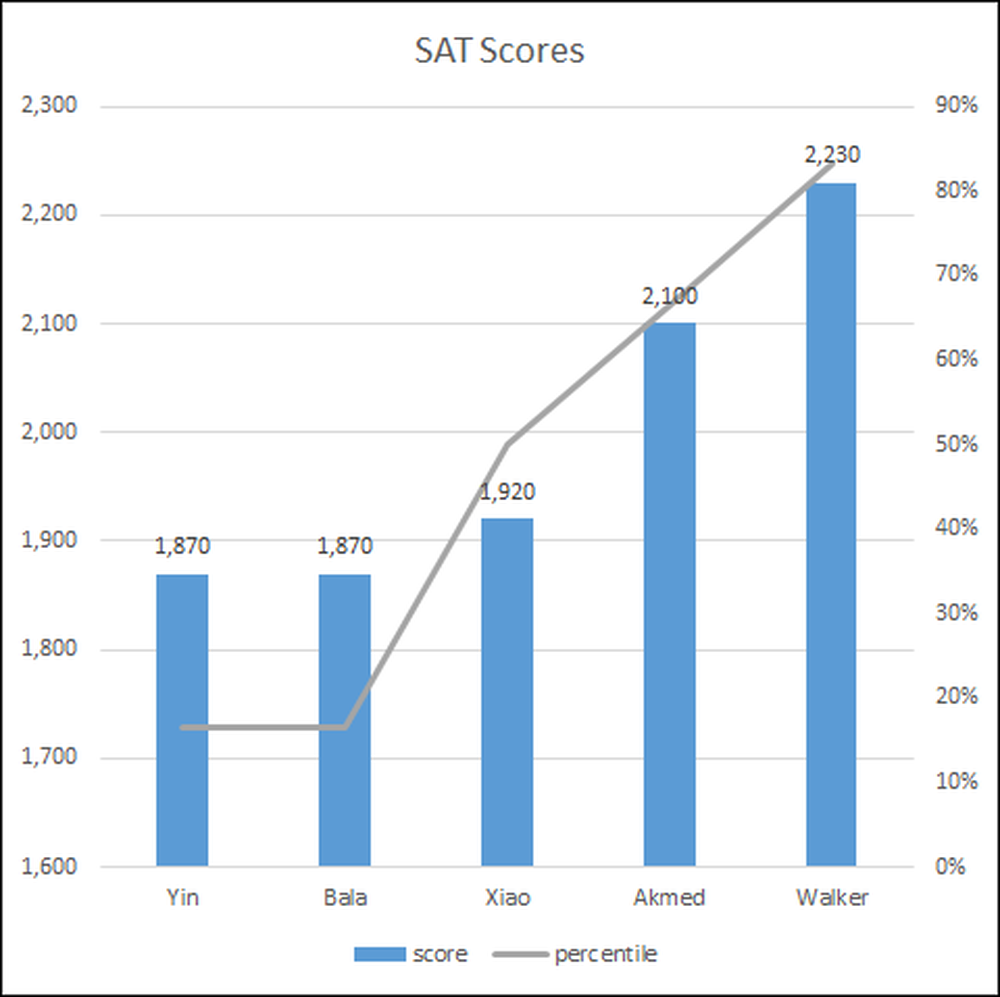
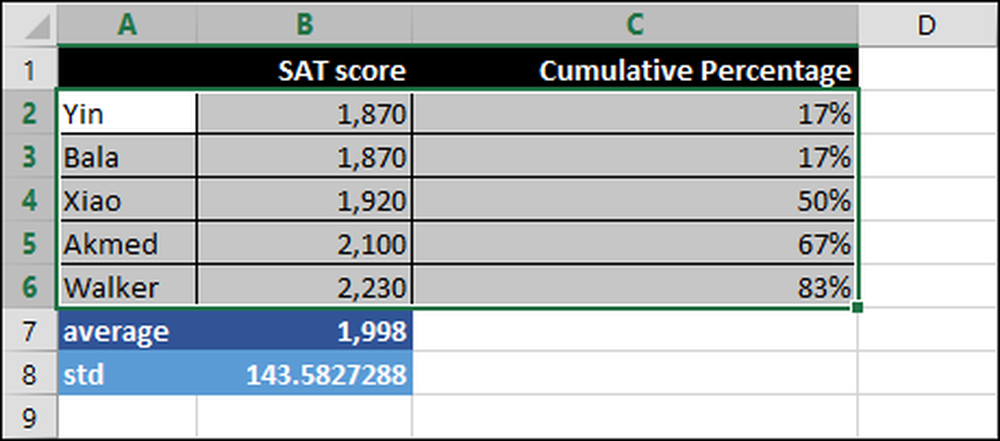
Uczniowie są na osi poziomej, a ich wyniki SAT są wyświetlane jako niebieski wykres słupkowy na skali (oś pionowa) od 1600 do 2300.

Ranking percentyla jest prawą osią pionową od 0 do 90 procent i jest reprezentowany przez szarą linię.

Jak utworzyć wykres

Tworzenie wykresu jest tematem samym w sobie, jednak wyjaśnimy pokrótce, jak powstał powyższy wykres.

Najpierw wybierz zakres komórek, które mają być na wykresie. W tym przypadku A2 do C6, ponieważ chcemy numerów, jak również nazwisk uczniów.

Z menu "Wstaw" wybierz "Wykresy" -> "Polecane wykresy":

Komputer zaleca wykres "Clustered-Column, Secondary Axis". Część "Druga oś" oznacza, że ​​rysuje dwie osie pionowe. W tym przypadku ten wykres jest tym, który chcemy. Nie musimy robić nic więcej.

Możesz użyć przesuwania wykresu dookoła i zmieniać jego rozmiar, aż uzyskasz go w rozmiarze i położeniu, które chcesz. Gdy będziesz zadowolony, możesz zapisać wykres w arkuszu kalkulacyjnym.

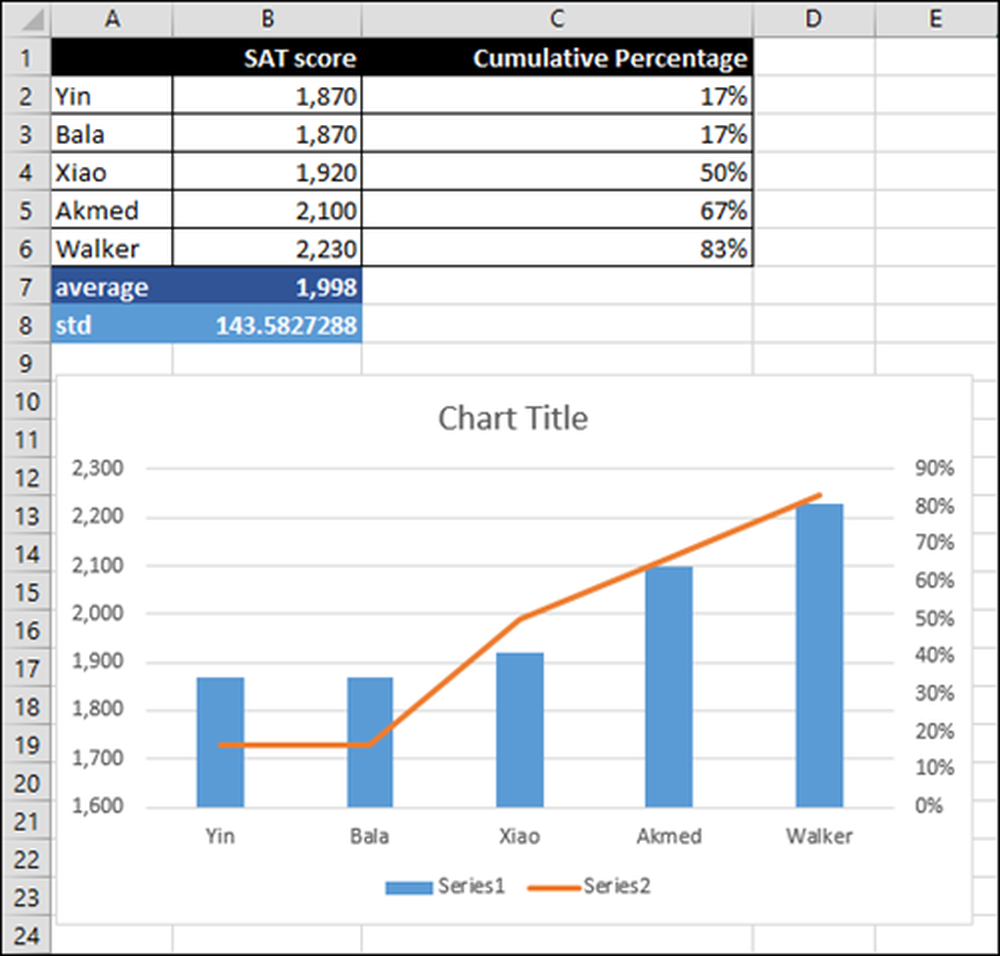
Jeśli klikniesz prawym przyciskiem myszy na wykresie, a następnie "Wybierz dane", zobaczysz, jakie dane są wybrane dla zakresu.

Funkcja "Zalecane wykresy" zwykle eliminuje konieczność radzenia sobie z takimi skomplikowanymi szczegółami, jak określanie danych, które mają być dołączane, przypisywanie etykiet i przypisywanie lewej i prawej osi pionowej.

W oknie dialogowym "Select Data Source" kliknij "score" w "Legend Entries (Series)" i naciśnij "Edit", i zmień je, aby powiedzieć "Score".

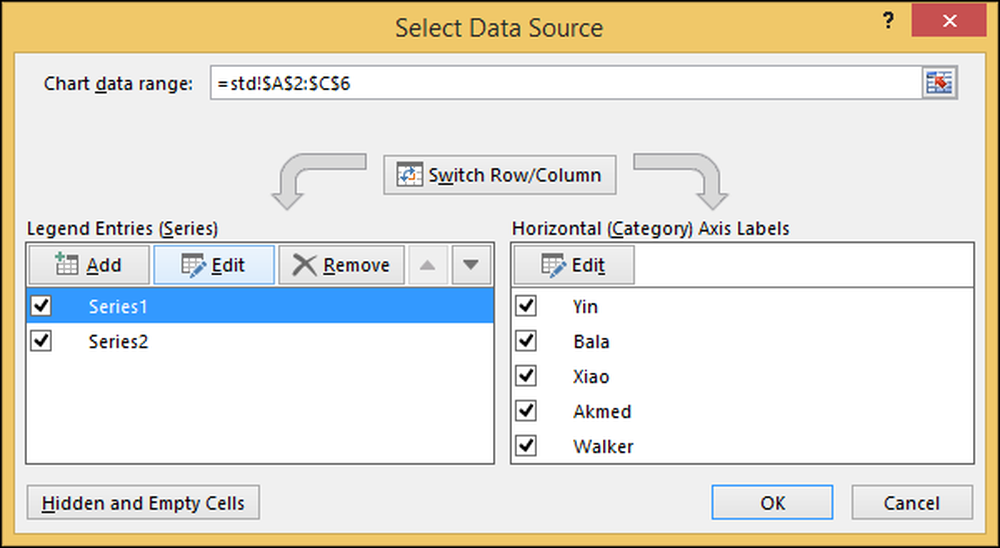
Następnie zmień serię 2 ("percentyl") na "Percentyl".

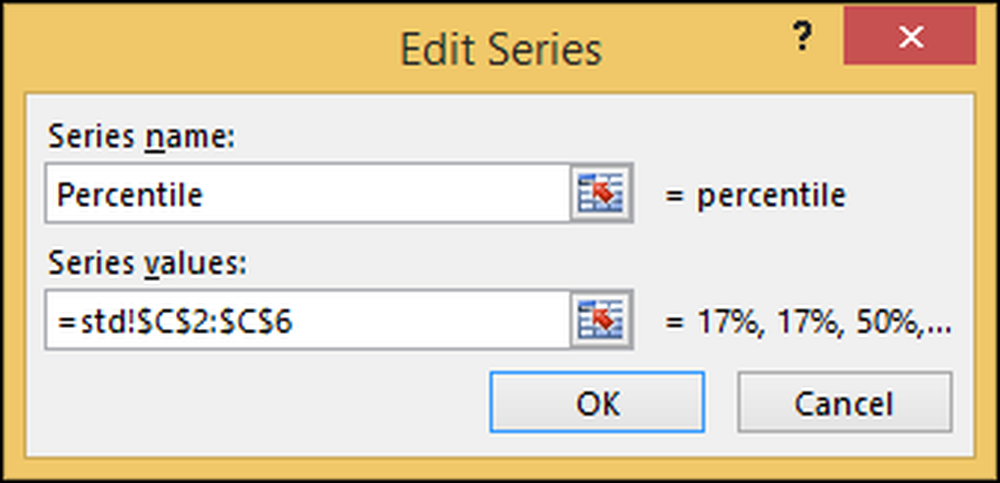
Wróć do swojego wykresu i kliknij "Tytuł wykresu" i zmień go na "Wyniki SAT". Teraz mamy pełną tabelę. Posiada dwie osie poziome: jedną dla wyniku SAT (niebieska) i jedną dla skumulowanego procentu (pomarańczowa).

Przykład: problem z transportem

Problem transportu jest klasycznym przykładem rodzaju matematyki zwanym "programowaniem liniowym". Pozwala to zmaksymalizować lub zminimalizować wartość podlegającą pewnym ograniczeniom. Ma wiele aplikacji do szerokiej gamy problemów biznesowych, dlatego warto dowiedzieć się, jak to działa.

Zanim zaczniemy od tego przykładu, musimy włączyć opcję "Excel Solver".

Włącz dodatek do dodatku Solver

Wybierz "Plik" -> "Opcje" -> "Dodatki". U dołu opcji dodatków kliknij przycisk "Przejdź" obok opcji "Zarządzaj: Dodatki do programu Excel".

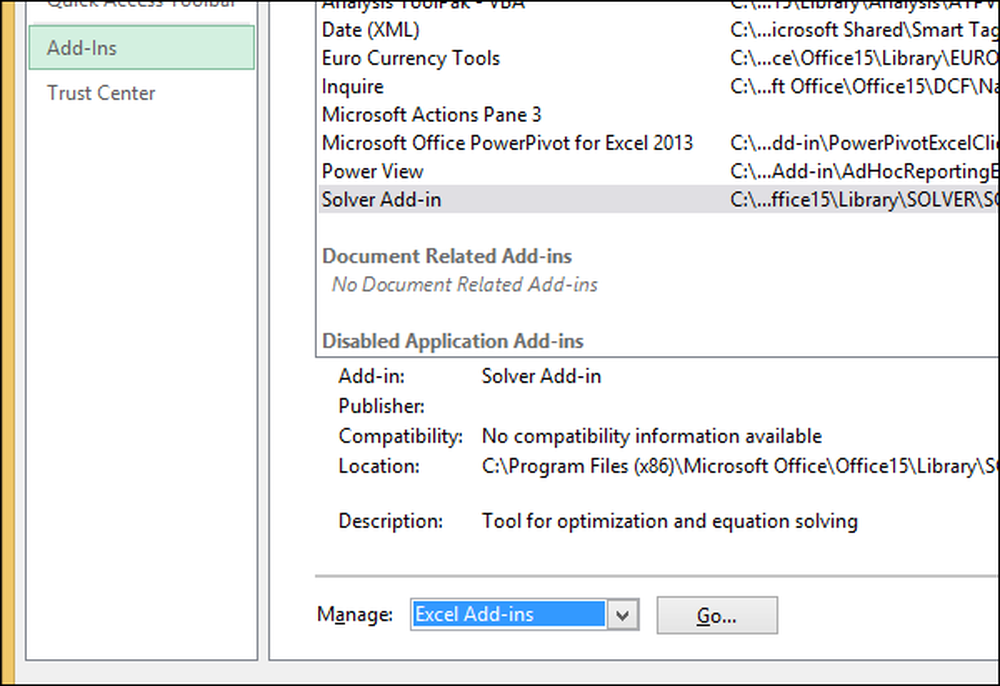
W wyświetlonym menu kliknij pole wyboru, aby włączyć opcję "Dodatek Solver" i kliknij "OK".

Przykład: Oblicz najniższe koszty wysyłki iPada

Załóżmy, że wysyłamy iPady i staramy się wypełnić nasze centra dystrybucji, korzystając z najniższych kosztów transportu. Mamy umowę z firmą przewozową i lotniczą, która wysyła iPady z Szanghaju, Pekinu i Hongkongu do centrów dystrybucji przedstawionych poniżej.

Cena wysyłki każdego iPada to odległość od fabryki do centrum dystrybucji do zakładu podzielona przez 20 000 kilometrów. Na przykład jest to 8,024 km od Szanghaju do Melbourne, które wynosi 8,024 / 20 000 lub 0,40 USD na iPada.

Pytanie brzmi, w jaki sposób wysyłać wszystkie te iPady z tych trzech zakładów do tych czterech miejsc docelowych po najniższych możliwych kosztach?

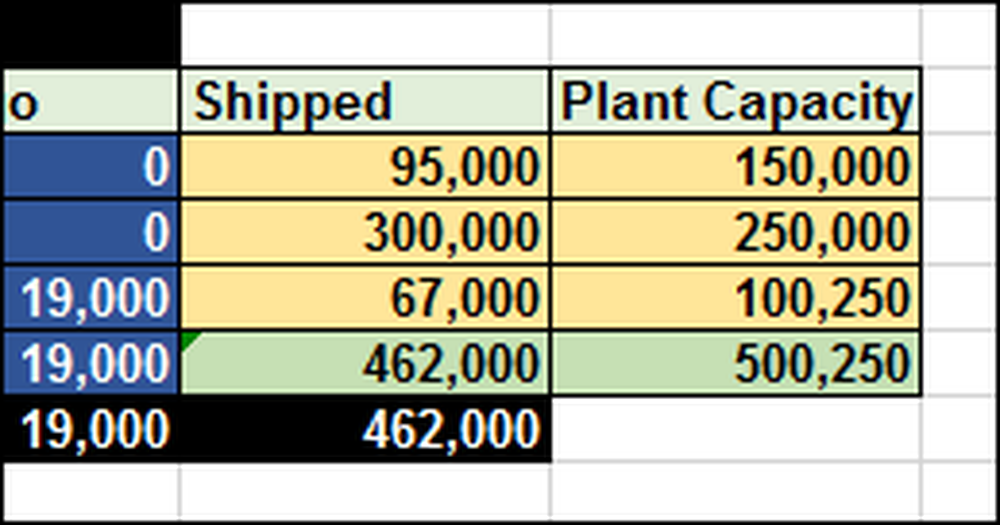
Jak możesz sobie wyobrazić, ustalenie tego może być bardzo trudne bez jakiejś formuły i narzędzia. W tym przypadku musimy wysłać łącznie 462 000 (F12) wszystkich iPadów. Rośliny mają ograniczoną pojemność 500 250 jednostek (G12).

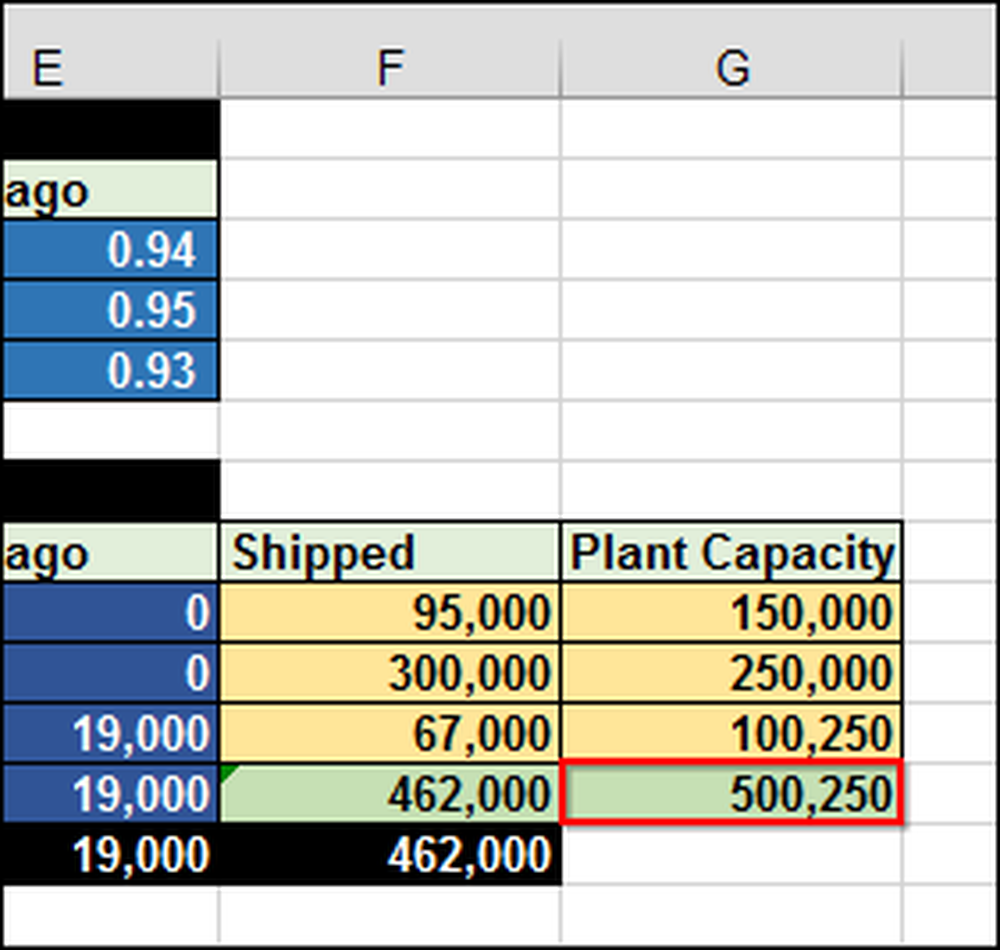
W arkuszu kalkulacyjnym, aby zobaczyć, jak to działa, wpisaliśmy 1 w komórce B10, co oznacza, że ​​chcemy wysłać 1 iPada z Szanghaju do Melbourne. Ponieważ koszty transportu na tej trasie wynoszą 0,40 USD za iPada, całkowity koszt (B17) wynosi 0,40 USD.

Liczba została obliczona za pomocą funkcji = SUMPRODUCT (koszty, wysłane) "koszty" to zakresy B3: E5.

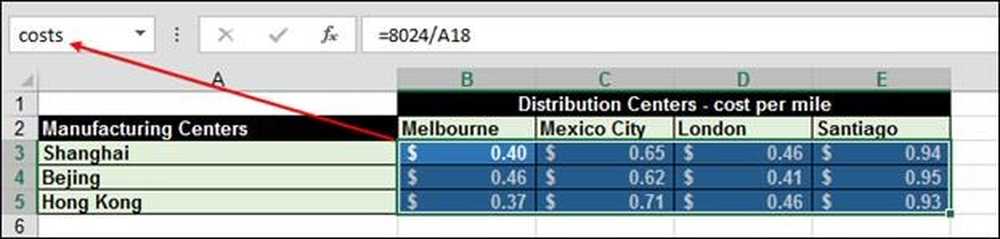
A "wysłane" to zakres B9: E11:

SUMPRODUCT mnoży "koszty" razy w przedziale "wysłane" (B14). To się nazywa "mnożenie macierzy".

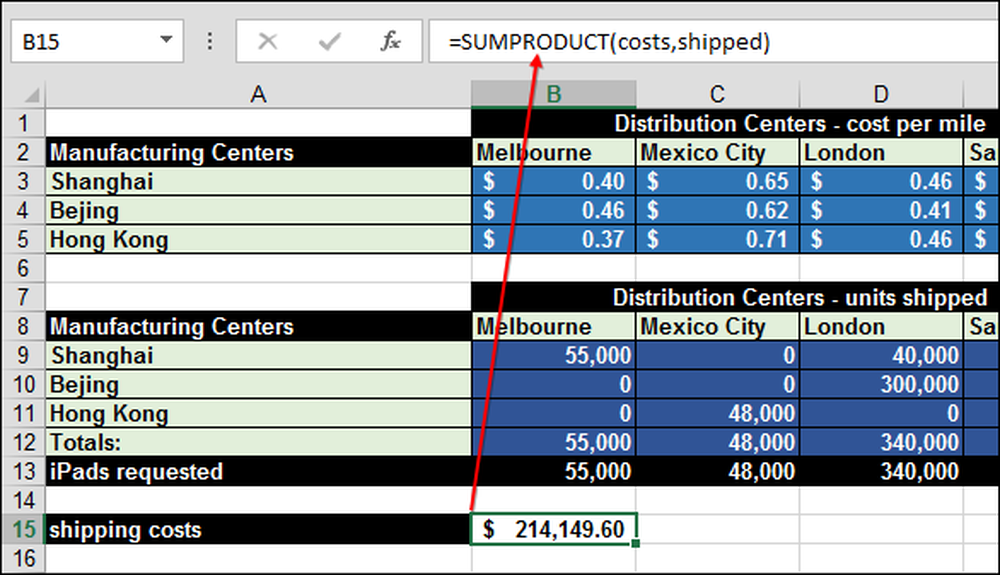
Aby SUMPRODUCT działał poprawnie, dwie macierze - koszty i wysłane - muszą być tej samej wielkości. Możesz obejść to ograniczenie, wykonując dodatkowe koszty i koszty wysyłki kolumn i wierszy o zerowej wartości, dzięki czemu tablice są tej samej wielkości i nie ma wpływu na całkowite koszty.

Korzystanie z Solvera

Gdybyśmy tylko musieli zrobić, to pomnożyć macierze "koszty" razy "wysłane", które nie byłyby zbyt skomplikowane, ale musimy też poradzić sobie z ograniczeniami.

Musimy wysłać to, czego wymaga każde centrum dystrybucji. Wstawiamy tę stałą do solwera w ten sposób: $ B 12 $: 12 $ = 13 $ 13 $: 13 $. Oznacza to, że suma wysłanych, tj. Sumy w komórkach $ B 12 $: 12 $, musi być większa lub równa wartości wymaganej przez każde centrum dystrybucyjne ($ B 13: $ E 13 $).

Nie możemy wysyłać więcej niż produkujemy. Piszemy takie ograniczenia: $ F 9: $ F 11 $ <= $G$9:$G$11. Put another way, what we ship from each plant $F$9:$F$11 cannot exceed (must be less than or equal to) the capacity of each plant: $G$9:$G$11.

Teraz przejdź do menu "Dane" i naciśnij przycisk "Solver". Jeśli nie ma przycisku "Solver", musisz włączyć dodatek Solver.

Wpisz dwa ograniczenia szczegółowe wcześniej i wybierz zakres "Przesyłki", który jest zakresem liczb, które Excel ma obliczyć. Wybierz także domyślny algorytm "Simplex LP" i wskaż, że chcemy "zminimalizować" komórkę B15 ("całkowite koszty wysyłki"), gdzie jest napisane "Ustaw cel".

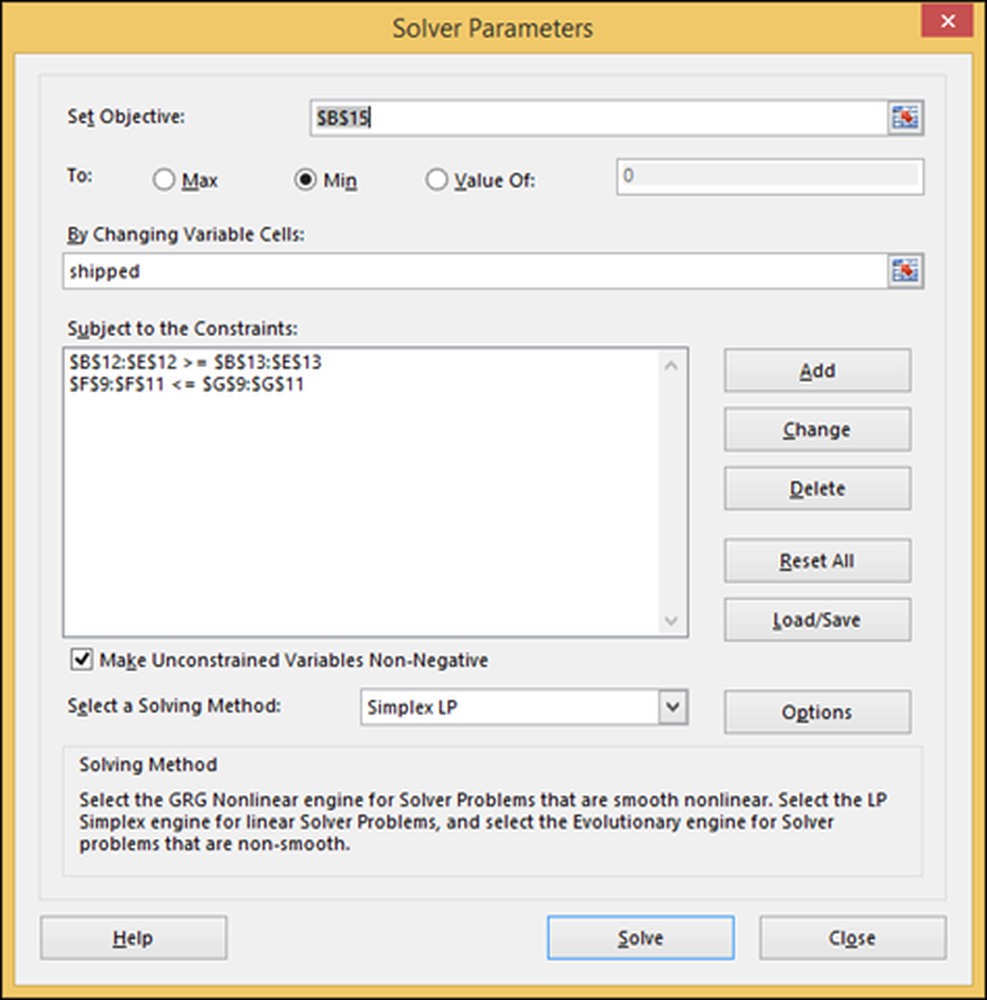
Naciśnij "Rozwiąż", a Excel zapisze wyniki w arkuszu kalkulacyjnym, czego właśnie chcemy. Możesz także zapisać to, abyś mógł bawić się z innymi scenariuszami.

Jeśli komputer twierdzi, że nie może znaleźć rozwiązania, zrobiłeś coś, co nie jest logiczne, na przykład, możesz poprosić o więcej iPadów niż może produkować roślina.

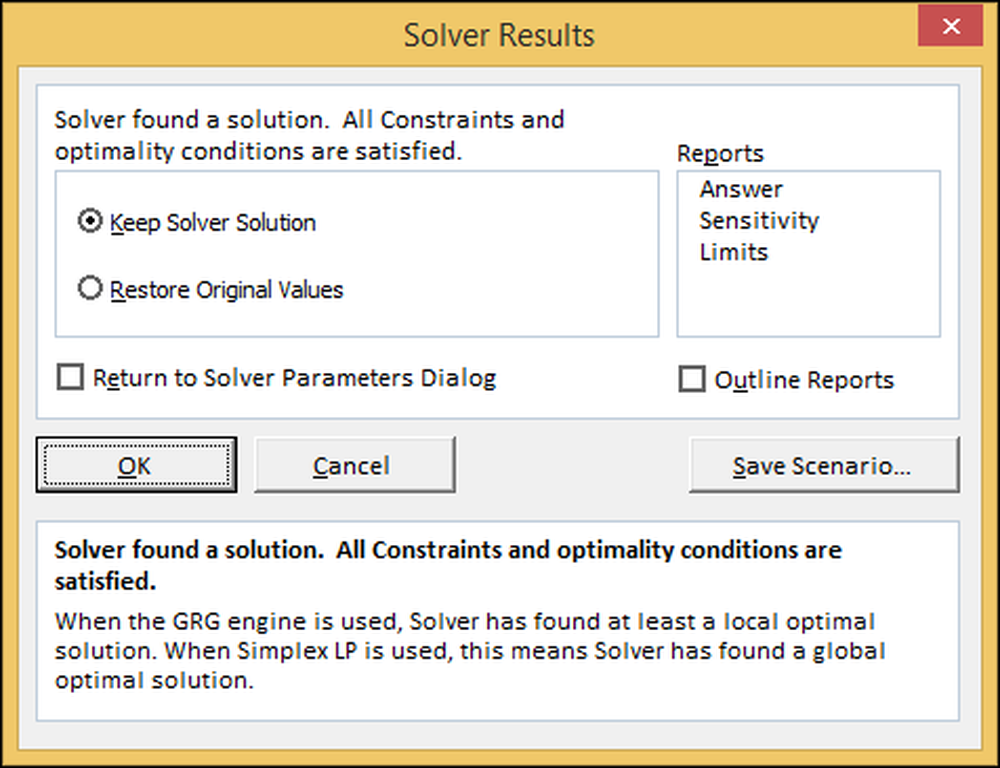
Tutaj Excel mówi, że znalazł rozwiązanie. Naciśnij "OK", aby zachować rozwiązanie i wrócić do arkusza kalkulacyjnego.

Przykład: wartość bieżąca netto

W jaki sposób firma decyduje się zainwestować w nowy projekt? Jeżeli "wartość bieżąca netto" (NPV) jest dodatnia, inwestują w nią. Jest to standardowe podejście większości analityków finansowych.

Załóżmy na przykład, że firma wydobywcza Codelco chce rozbudować kopalnię miedzi Andinas. Standardowym podejściem do ustalenia, czy kontynuować projekt, jest obliczenie wartości bieżącej netto. Jeśli NPV jest większa od zera, wówczas projekt będzie opłacalny, biorąc pod uwagę dwa nakłady (1) i (2) koszt kapitału.

Mówiąc prosto po angielsku, koszt kapitału oznacza, ile by zarobiły te pieniądze, gdyby tylko zostawił je w banku. Używasz kosztu kapitału do zdyskontowania wartości pieniężnych, aby przedstawić wartość, innymi słowy 100 $ w ciągu pięciu lat może dzisiaj wynosić 80 $.

W pierwszym roku 45 milionów dolarów jest zarezerwowane jako kapitał na sfinansowanie projektu. Księgowi ustalili, że ich koszt kapitału wynosi sześć procent.

Po rozpoczęciu wydobycia zaczyna się gotówka, ponieważ firma znajduje i sprzedaje wyprodukowaną przez siebie miedź. Oczywiście, im więcej kopalnią, tym więcej pieniędzy zarabiają, a ich prognoza pokazuje, że ich przepływ gotówki wzrasta, aż osiągnie 9 milionów dolarów rocznie.

Po 13 latach NPV wynosi 3 945 074 USD, więc projekt będzie opłacalny. Według analityków finansowych "okres spłaty" wynosi 13 lat.

Tworzenie tabeli przestawnej

"Tabela przestawna" to w zasadzie raport. Nazywamy je tabelami przestawnymi, ponieważ można łatwo zmienić je w jeden typ raportu na inny bez konieczności tworzenia całego nowego raportu. Więc oni sworzeń w miejscu. Pokażmy podstawowy przykład, który uczy podstawowych pojęć.

Przykład: raporty sprzedaży

Sprzedawcy są bardzo konkurencyjni (to część bycia sprzedawcą), więc naturalnie chcą wiedzieć, jak sobie radzą pod koniec kwartału i końca roku, a także ile ich prowizji będzie.

Załóżmy, że mamy trzech sprzedawców - Carlosa, Freda i Julie - wszystkie sprzedające się ropę naftową. Ich sprzedaż w dolarach za kwartał fiskalny w 2014 r. Została przedstawiona w poniższym arkuszu kalkulacyjnym.

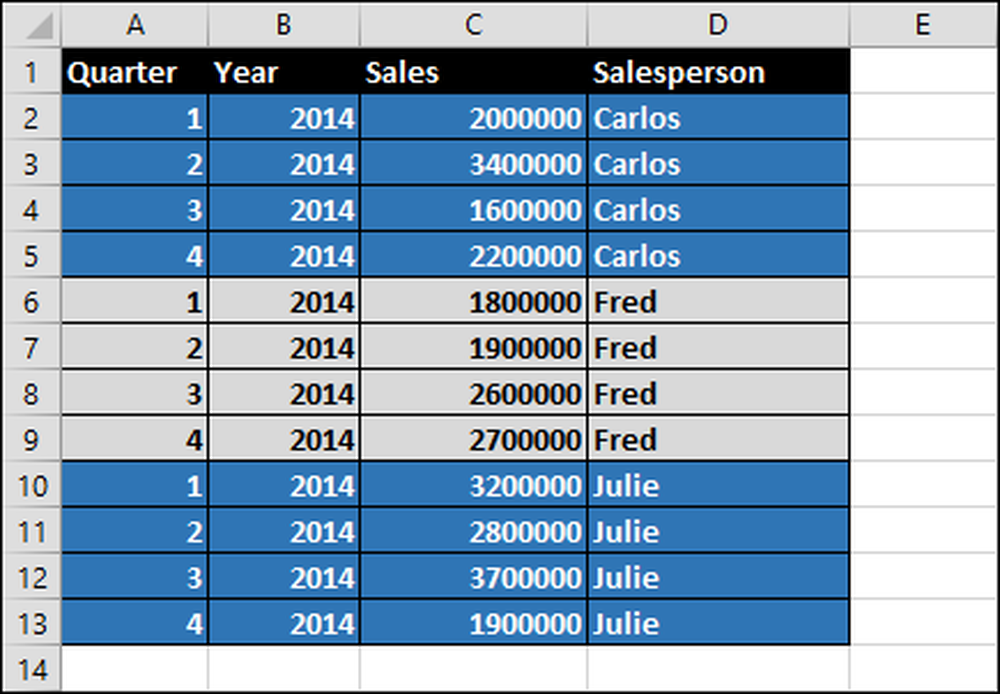
Aby wygenerować te raporty, tworzymy tabelę przestawną:

Wybierz "Wstaw -> Tabela przestawna, znajduje się po lewej stronie paska narzędzi:

Wybierz wszystkie wiersze i kolumny (łącznie z nazwą sprzedawcy), jak pokazano poniżej:

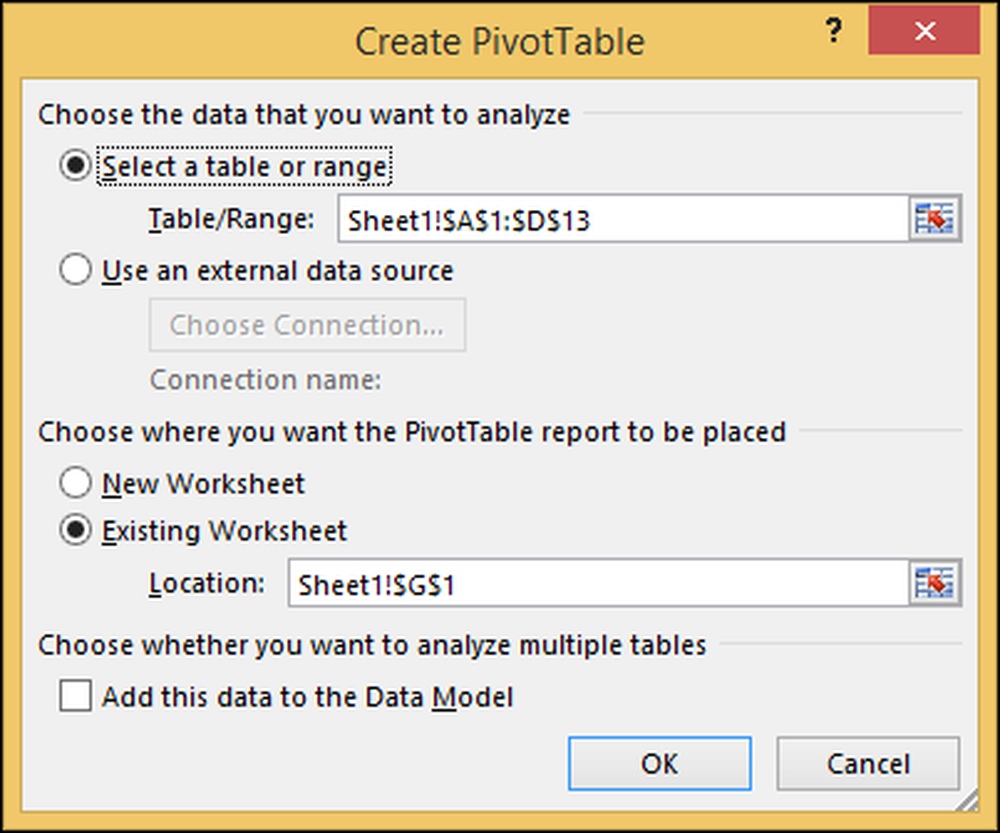
Okno dialogowe tabeli przestawnej pojawi się po prawej stronie arkusza kalkulacyjnego.

Po kliknięciu wszystkich czterech pól w oknie dialogowym tabeli przestawnej (kwartał, rok, sprzedaż i sprzedawca) program Excel dodaje do arkusza kalkulacyjnego raport, który nie ma sensu, ale dlaczego?

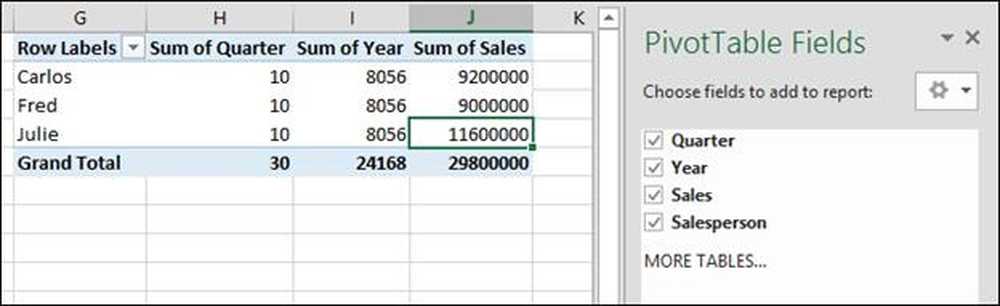
Jak widać, wybraliśmy wszystkie cztery pola do dodania do raportu. Domyślnym zachowaniem programu Excel jest grupowanie wierszy według pól tekstowych, a następnie sumowanie wszystkich pozostałych wierszy.

Tutaj daje nam sumę roku 2014 + 2014 + 2014 + 2014 = 24 168, co jest nonsensem. Dał także sumę ćwiartek 1 + 2 + 3 + 4 = 10 * 3 = 3 0. Nie potrzebujemy tych informacji, więc usuwamy zaznaczenie tych pól, aby je usunąć z naszej tabeli przestawnej.

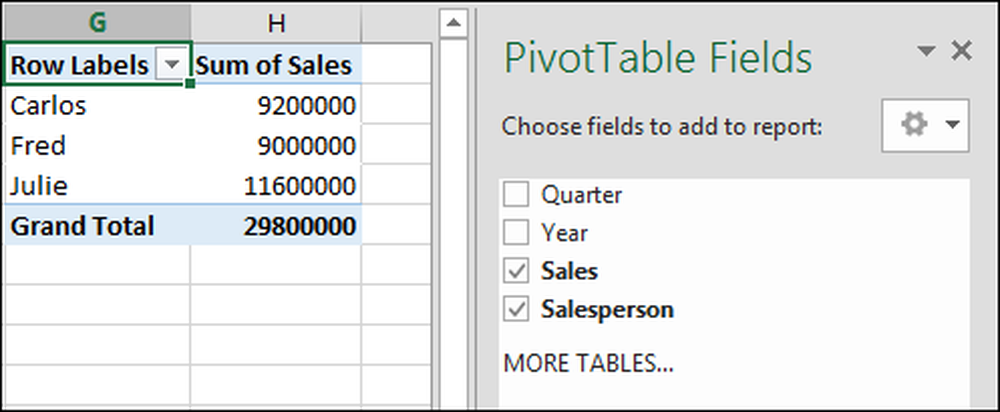
"Suma sprzedaży" (całkowita sprzedaż) jest jednak istotna, więc naprawimy to.

Przykład: Sprzedaż przez sprzedawcę

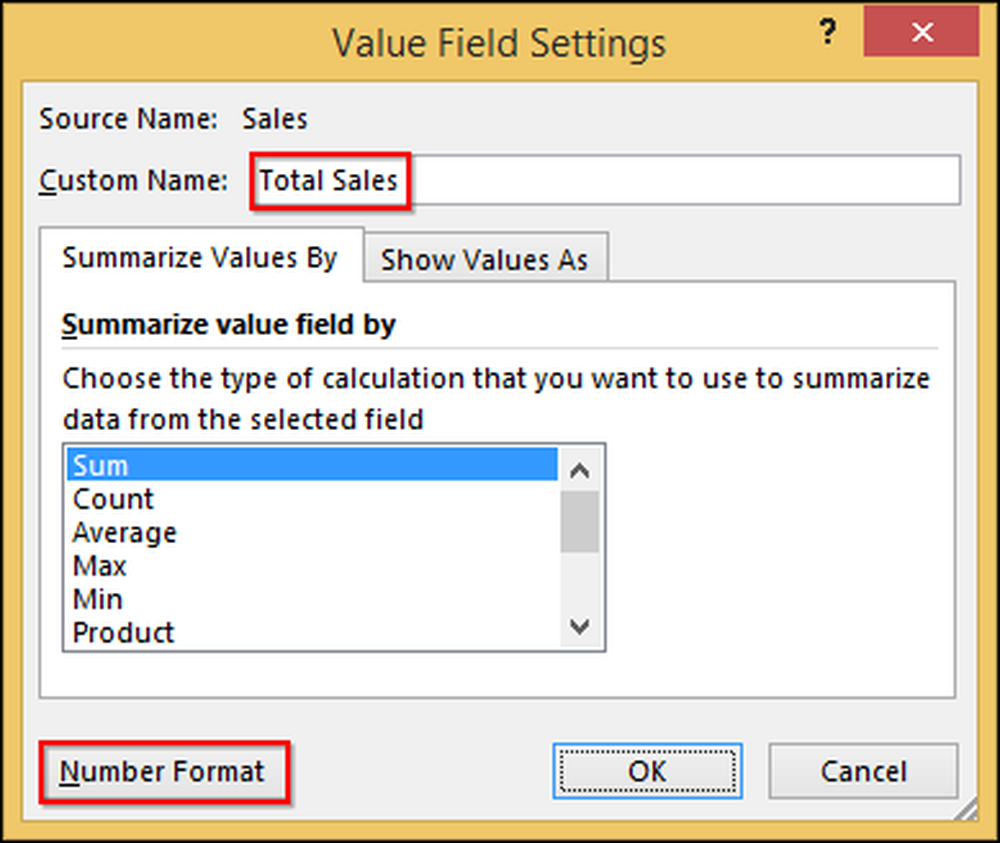
Możesz edytować "Suma sprzedaży", która mówi "Całkowita sprzedaż", która jest bardziej przejrzysta. Możesz także sformatować komórki jako walutę tak, jak sformatowałbyś inne komórki. Najpierw kliknij "Suma sprzedaży" i wybierz "Ustawienia wartości pola".

W wynikowym oknie dialogowym zmieniamy nazwę na "Całkowita sprzedaż", następnie klikamy "Format liczbowy" i zmieniamy go na "Waluta".

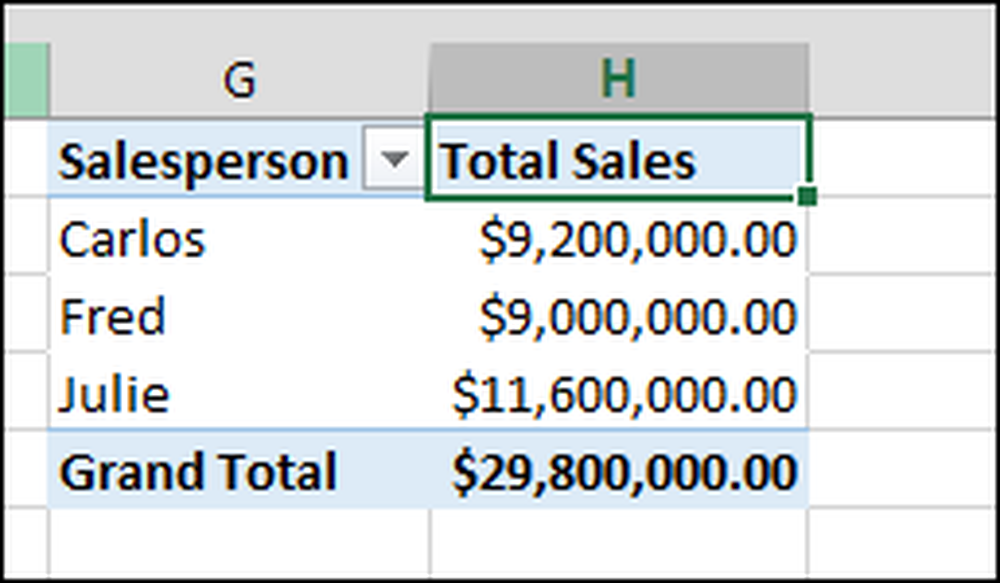
Następnie możesz zobaczyć swoje dzieło w tabeli przestawnej:

Przykład: sprzedaż przez sprzedawcę i kwartał

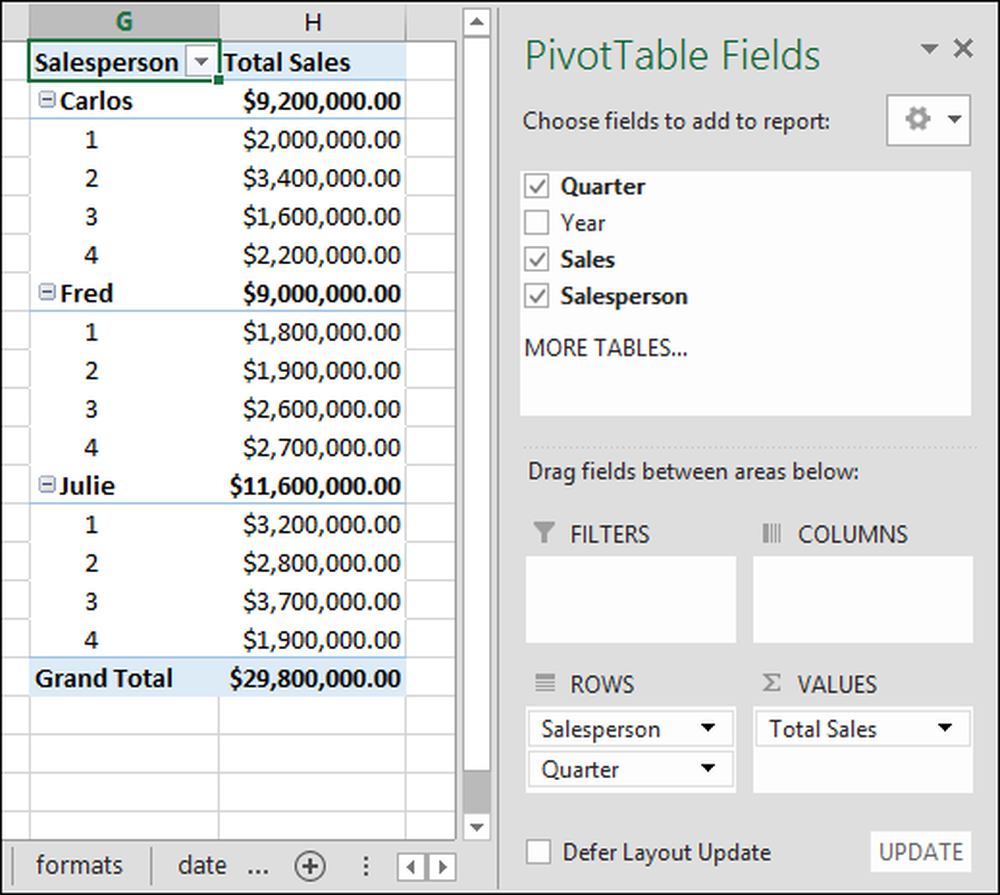
Teraz dodajmy sumy cząstkowe dla każdego kwartału. Aby dodać podsumy, kliknij lewym przyciskiem myszy pole "Kwartał" i przytrzymaj i przeciągnij do sekcji "wiersze". Możesz zobaczyć wynik na zrzucie ekranu poniżej:

Kiedy już to zrobimy, usuńmy wartości "sumy kwartałów". Wystarczy kliknąć strzałkę i kliknąć "Usuń pole". Na zrzucie ekranu widać teraz, że dodaliśmy wiersze "Kwartał", które dzielą sprzedaż każdego sprzedawcy według kwartału.

Mając na uwadze te umiejętności, możesz teraz tworzyć tabele przestawne na podstawie własnych danych!

Wniosek

Podsumowując, pokazaliśmy niektóre funkcje formuł i funkcji Microsoft Excel, które można zastosować w programie Microsoft Excel do potrzeb biznesowych, akademickich lub innych potrzeb.

Jak widzieliśmy, program Microsoft Excel jest ogromnym produktem z tak wieloma funkcjami, że większość ludzi, nawet zaawansowanych użytkowników, nie zna ich wszystkich. Niektórzy ludzie mogą powiedzieć, że to skomplikowane; uważamy, że jest bardziej wszechstronny.

Mamy nadzieję, że przedstawiając wiele przykładów z życia, zademonstrowaliśmy nie tylko funkcje dostępne w programie Microsoft Excel, ale nauczyliśmy Cię czegoś o statystykach, programowaniu liniowym, tworzeniu wykresów, losowaniu liczb i innych pomysłach, które możesz teraz przyjąć i używać w swojej szkole lub w miejscu pracy.

Pamiętaj, że jeśli chcesz wrócić i ponownie wziąć udział w zajęciach, możesz zacząć od nowa w Lekcji 1!